
題目列表(包括答案和解析)
22.
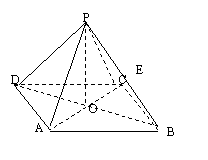
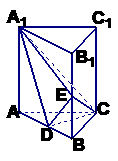
如圖所示:正四棱錐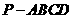 中,側(cè)棱
中,側(cè)棱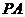 與底面
與底面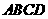 所成的角的正切值為
所成的角的正切值為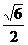 ,
,
(1)求側(cè)面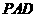 與底面
與底面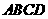 所成的二面角的大小;
所成的二面角的大小;
 (2)若E是
(2)若E是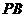 的中點,求異面直線PD與AE所成角的正切值;
的中點,求異面直線PD與AE所成角的正切值;
(3)在側(cè)面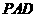 上尋找一點F,使EF⊥側(cè)面
上尋找一點F,使EF⊥側(cè)面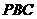 ,試確定點
,試確定點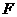 的位置,并加以證明.
的位置,并加以證明.
21. 如圖,四棱錐P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD為直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.點E在棱PA上,且PE=2EA.
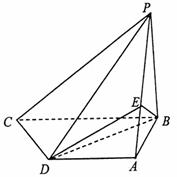 (1)求異面直線PA與CD所成的角;
(1)求異面直線PA與CD所成的角;
(2)求證:PC∥平面EBD;
(3)求二面角A-BE-D的大小.(用反三角函數(shù)表示).
20. 如圖,直三棱柱ABC-A B
B C
C 中,AC=BC=AA
中,AC=BC=AA =2,
=2, 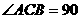
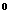 ,E為BB
,E為BB 中
中
點,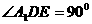 .
.
(1)求證:CD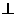 面A
面A ABB
ABB ;
;
(2)求二面角C-A E-D的大小.
E-D的大小.
19.
已知在四面體ABCD中,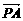 = a,
= a,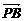 = b,
= b,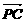 = c,G∈平面ABC.
= c,G∈平面ABC.
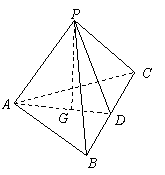 (1)若G為△ABC的重心,試證明
(1)若G為△ABC的重心,試證明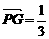 (a+b+c);
(a+b+c);
(2)試問(1)的逆命題是否成立?并證明你的結(jié)論.
18. 如圖為某一幾何體的展開圖,其中ABCD是邊長為6的正方形,SD=PD=6,CR=SC,AQ=AP,點S、D、A、Q及P、D、C、R共線.
(1)沿圖中虛線將它們折疊起業(yè),使P、Q、R、S四點重合,請畫出其直觀圖,試問需要幾個這樣的幾何體才能拼成一個棱長為6的正方體ABCD-A1B1C1D1?
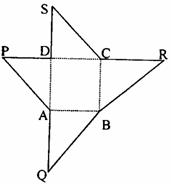 (2)設正方體ABCD-A1B1C1D1的棱CC1的中點為E,求平面AB1E與平面ABC所成二面角(銳角)的余弦值.
(2)設正方體ABCD-A1B1C1D1的棱CC1的中點為E,求平面AB1E與平面ABC所成二面角(銳角)的余弦值.
17.
已知定點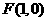 ,動點
,動點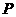 (異于原點)在
(異于原點)在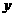 軸上運動,連接PF,過點
軸上運動,連接PF,過點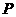 作
作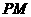 交
交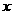 軸于點
軸于點 ,并延長
,并延長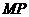 到點
到點 ,且
,且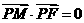 ,
,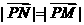 .
.
(1)求動點 的軌跡
的軌跡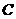 的方程;
的方程;
(2)若直線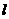 與動點
與動點 的軌跡交于
的軌跡交于 、
、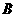 兩點,若
兩點,若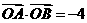 且
且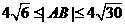 ,求直線
,求直線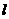 的斜率
的斜率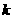 的取值范圍.
的取值范圍.
16. 在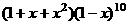 的展開式中,
的展開式中,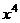 項的系數(shù)是
項的系數(shù)是
15. 某學校要從高三的6個班中派9名同學參加市中學生外語口語演講,每班至少派1人,則這9個名額的分配方案共有 種.(用數(shù)字作答)
14. 一個正方體的棱長為2,將八個直徑各為1的球放進去之后,正中央空間能放下的最大的球的直徑為__________________.
13. 若橢圓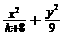 =1的離心率為
=1的離心率為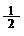 ,則k的值為 .
,則k的值為 .
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com