
題目列表(包括答案和解析)
6.
方程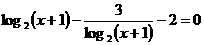 的解是
的解是 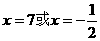 。
。
5.
函數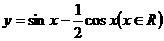 的最大值為
的最大值為 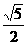 。
。
4.
設復數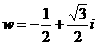 ,則
,則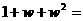
 。
。
3.
函數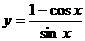 的最小正周期是
的最小正周期是 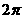 。
。
2.
已知集合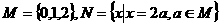 ,則集合
,則集合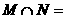
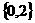 。
。
1.
函數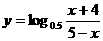 的定義域為
的定義域為 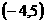 。
。
22、已知二次函數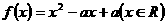 同時滿足:①不等式
同時滿足:①不等式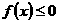 的解集有且只有一個元素;②在定義域內存在
的解集有且只有一個元素;②在定義域內存在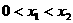 ,使得不等式
,使得不等式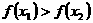 成立。
成立。
設數列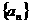 的前
的前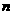 項和
項和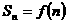 ,
,
(1)求數列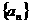 的通項公式;
的通項公式;
(2)試構造一個數列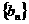 ,(寫出
,(寫出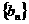 的一個通項公式)滿足:對任意的正整數
的一個通項公式)滿足:對任意的正整數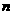 都有
都有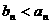 ,且
,且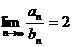 ,并說明理由;
,并說明理由;
(3)設各項均不為零的數列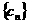 中,所有滿足
中,所有滿足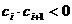 的正整數
的正整數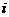 的個數稱為這個數列
的個數稱為這個數列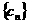 的變號數。令
的變號數。令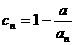 (
(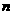 為正整數),求數列
為正整數),求數列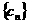 的變號數。
的變號數。
解:(1)∵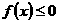 的解集有且只有一個元素,∴
的解集有且只有一個元素,∴ ,
,
當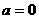 時,函數
時,函數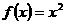 在
在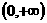 上遞增,故不存在
上遞增,故不存在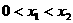 ,使得不等式
,使得不等式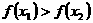 成立。
成立。
當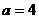 時,函數
時,函數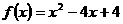 在
在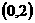 上遞減,故存在
上遞減,故存在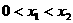 ,使得不等式
,使得不等式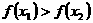 成立。
成立。
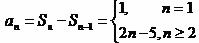 綜上,得
綜上,得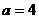 ,
,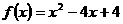 ,∴
,∴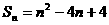 ,∴
,∴
(2)要使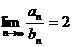 ,可構造數列
,可構造數列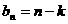 ,∵對任意的正整數
,∵對任意的正整數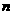 都有
都有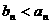 ,
,
∴當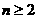 時,
時,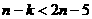 恒成立,即
恒成立,即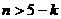 恒成立,即
恒成立,即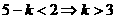 ,
,
又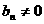 ,∴
,∴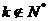 ,∴
,∴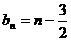 ,等等。
,等等。
(3)解法一:由題設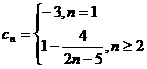 ,
,
∵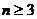 時,
時,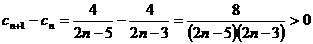 ,∴
,∴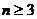 時,數列
時,數列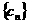 遞增,
遞增,
∵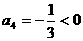 ,由
,由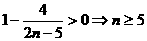 ,可知
,可知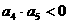 ,即
,即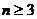 時,有且只有
時,有且只有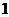 個變號數;
個變號數;
又∵ ,即
,即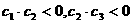 ,∴此處變號數有
,∴此處變號數有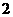 個。
個。
綜上得 數列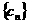 共有
共有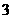 個變號數,即變號數為
個變號數,即變號數為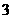 。
。
解法二:由題設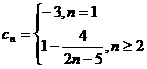 ,
,
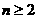 時,令
時,令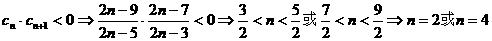 ;
;
又∵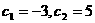 ,∴
,∴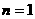 時也有
時也有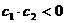 。
。
綜上得 數列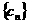 共有
共有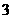 個變號數,即變號數為
個變號數,即變號數為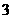 。
。
21、設函數 ,函數
,函數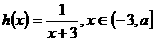 ,其中
,其中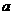 為常數且
為常數且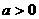 ,令函數
,令函數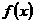 為函數
為函數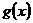 和
和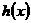 的積函數。
的積函數。
(1)求函數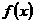 的表達式,并求其定義域;
的表達式,并求其定義域;
(2)當 時,求函數
時,求函數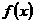 的值域;
的值域;
(3)是否存在自然數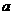 ,使得函數
,使得函數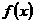 的值域恰為
的值域恰為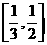 ?若存在,試寫出所有滿足條件的自然數
?若存在,試寫出所有滿足條件的自然數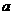 所構成的集合;若不存在,試說明理由。
所構成的集合;若不存在,試說明理由。
解:(1)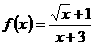 ,
,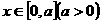 。
。
(2)∵ ,∴函數
,∴函數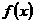 的定義域為
的定義域為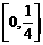 ,令
,令 ,則
,則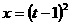 ,
,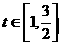 ,
,
∴ ,
,
∵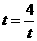 時,
時,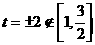 ,又
,又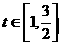 時,
時,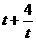 遞減,∴
遞減,∴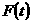 單調遞增,
單調遞增,
∴ ,即函數
,即函數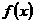 的值域為
的值域為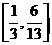 。
。
(3)假設存在這樣的自然數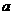 滿足條件,令
滿足條件,令 ,則
,則 ,
,
∵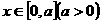 ,則
,則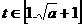 ,要滿足值域為
,要滿足值域為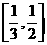 ,則要滿足
,則要滿足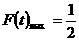 ,
,
由于當且僅當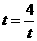
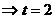 時,有
時,有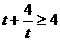 中的等號成立,且此時
中的等號成立,且此時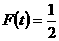 恰為最大值,
恰為最大值,
∴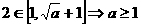 ,
,
又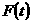 在
在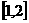 上是增函數,在
上是增函數,在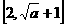 上是減函數,∴
上是減函數,∴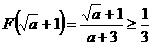
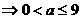 ,
,
綜上,得 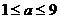 。
。
20、人口問題其實是許多國家的政府都要面對的問題。05年10月24日出版的《環(huán)球時報》就報道了一篇俄羅斯政府目前遭遇“人口危機”的文章。報道中引用了以下來自俄政府公布的數據:
●截至05年6月底,俄羅斯人口為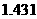 億,人口密度每平方公里只有
億,人口密度每平方公里只有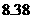 人;
人;
●04年一年俄人口就減少了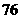 萬,05年1月至5月共又減少了
萬,05年1月至5月共又減少了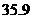 萬;
萬;
●據俄聯邦安全會議預測,到2050年,俄將只有約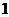 億人口,比目前銳減
億人口,比目前銳減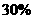 。
。
試根據以上數據信息回答下列問題:
(1)以04年至05年5月這17個月平均每月人口減少的數據為基礎,假設每月人口減少相同,預測到2050年6月底,俄羅斯的人口約為多少億?(保留三位小數)
(2)按第(1)小題給定的預測方法,到何時俄羅斯的人口密度將低于每平方公里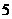 人?
人?
解:(1)由給出的信息可知,17個月里平均每月人口減少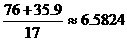 萬人,
萬人,
2005年6月底至2050年6月底共經過 個月,若每月人口減少數相同,
個月,若每月人口減少數相同,
則到2050年6月底俄羅斯的人口數約為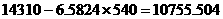 萬,即約為
萬,即約為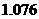 億。
億。
(2)設從05年6月底起,經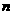 個月后俄羅斯的人口密度將低于每平方公里
個月后俄羅斯的人口密度將低于每平方公里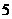 人,
人,
于是有 ,
,
∴至少要經過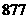 個月,即
個月,即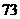 年零
年零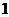 個月,也就是到2078年7月底,俄羅斯的人口密度將低于每平方公里
個月,也就是到2078年7月底,俄羅斯的人口密度將低于每平方公里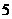 人。
人。
19、求證:不存在虛數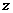 同時滿足:①
同時滿足:①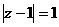 ;②
;②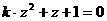 (
(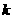 為實數且
為實數且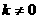 )。
)。
解:假設存在虛數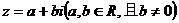 同時滿足兩個條件,
同時滿足兩個條件,
即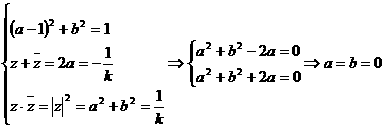 與假設
與假設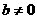 矛盾,
矛盾,
∴不存在虛數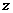 同時滿足①②兩個條件。
同時滿足①②兩個條件。
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com