
題目列表(包括答案和解析)
7.函數 在
在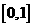 上的最大值和最小值之和為
上的最大值和最小值之和為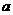 ,則
,則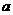 的值為(
)
的值為(
)
A.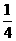 B.
B. C.
C.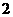 D.
D.
6.若函數 與函數
與函數 在區間
在區間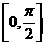 上的單調性相同,則
上的單調性相同,則 的一個值
的一個值
是 ( )
A.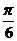 B.
B.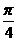 C.
C.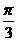 D.
D.
5.若直線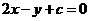 按向量
按向量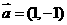 平移后與圓
平移后與圓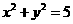 相切,則c的值為
( )
相切,則c的值為
( )
A.8或-2 B.6或-4 C.4或-6 D.2或-8
4.已知等差數列 的公差
的公差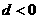 ,若
,若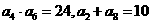 ,則該數列的前
,則該數列的前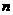 項和
項和
的最大值是 ( )
A. B.
B. C.
C. D.
D.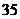
3.在等比數列 中,
中, ,
,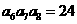 ,則
,則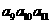 的值為
( )
的值為
( )
A. B.
B.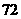 C.
C.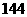 D.
D.
2.若向量 ,且
,且 ,則
,則 等于
( )
等于
( )
A.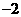 B.
B.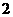 C.
C.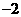 或
或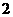 D.
D.
1.已知集合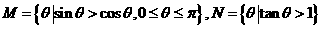 ,則
,則 等于(
)
等于(
)
A.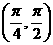 B.
B. C.
C.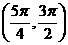 D.
D.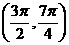
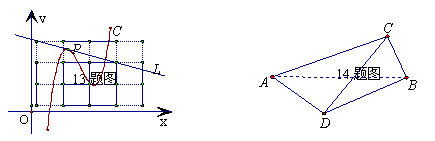
(13)在下圖中,直線L為曲線C在點P處的切線,則直線L的斜率是
(14)如圖,直角三角形ABC中,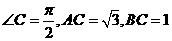 ,△ABD為等腰直角三角形,
,△ABD為等腰直角三角形, 。當點D到平面ABC距離最大時,直線CD與平面ABC所成角為___________
。當點D到平面ABC距離最大時,直線CD與平面ABC所成角為___________
(15)平面內滿足不等式組(x+y-4)(x+ 2y-6)≤0,x≥0,y≥0的所有點中,使目標函數z=5x+4y取得最大值的點的坐標是
(16)已知O為原點,點P (x、y)在單位圓x2 + y2 = 1上,點Q (2cosθ, 2sinθ)滿足
 =(
=(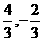 ),則
),則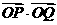 = ___________
= ___________
.三、解答題:本大題6個小題,共74分.解答必需寫出必要的文字說明、推理過程或計算步驟.
(17) 解不等式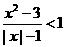
(18) 某公交公司對某線路客源情況統計顯示,公交車從每個停靠點出發后,乘客人數及頻率如下表:
|
人數 |
0~6 |
7~12 |
13~18 |
19~24 |
25~30 |
31人以上 |
|
頻率 |
0.1 |
0.15 |
0.25 |
0.20 |
0.20 |
0.1 |
(I)從每個停靠點出發后,乘客人數不超過24人的概率約是多少?
(II)全線途經10個停靠點,若有2個以上(含2個),乘客人數超過18人的概率大于0.9,公交公司就要考慮在該線路增加一個班次,請問該線路需要增加班次嗎?

(19) 在三棱柱 中,底面
中,底面 為正三角形,
為正三角形, ,
, 。
。
(I)求證: ;
;
(II)把四棱錐 繞直線
繞直線 旋轉到
旋轉到 ,使平面
,使平面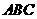 與平面
與平面 重合,試求旋轉過的角的余弦值。
重合,試求旋轉過的角的余弦值。
(20) 已知銳角α,β滿足2sinβ=sin(2α+β)且α+β≠ .
.
(I)求證:tan(α+β)=3tanα
(II)設y=tanβ, x=tanα, α∈[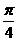 ,
, ]試求函數y=f (x)的最大值
]試求函數y=f (x)的最大值
(21) 設Sn為數列{an}的前n項和,如果Sn=2an-3n+5.
(I)證明:數列{an+3}是等比數列;
(II)是否存在正整數p、q、r(p<q<r)使得p,q, r和Sp,Sq,Sr同時成等差數列?若存在,求出p、q、r的值,若不存在,請說明理由。
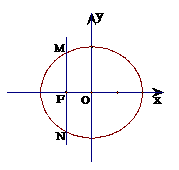
(22) (Ⅰ)橢圓 的左焦點為F,過F作垂直于x軸的直線與橢圓交于點M、N,相應的準線與x軸交于點H,求證:∠MHN為銳角,且直線MH與橢圓有且僅有一個公共點。
的左焦點為F,過F作垂直于x軸的直線與橢圓交于點M、N,相應的準線與x軸交于點H,求證:∠MHN為銳角,且直線MH與橢圓有且僅有一個公共點。
(Ⅱ)請針對拋物線y= ,類比(I),寫出一個真命題(不要求給出證明過程)。
,類比(I),寫出一個真命題(不要求給出證明過程)。
(Ⅲ)動直線l與(Ⅱ)中拋物線交于不同的兩點A、B,滿足 =m
=m (m∈R),拋物線在點A處的切線為l1,在點B處切線l2,切線l1與l2交點為T,求證:點T在準線上。
(m∈R),拋物線在點A處的切線為l1,在點B處切線l2,切線l1與l2交點為T,求證:點T在準線上。

絕密★啟用前
宿遷市2004-2005學年度高三年級第三次考試
12.經濟學中的“蛛網理論”(如圖),假定某種商品的“需求-價格”函數的圖象為直線l1,“供給-價格”函數的圖象為直線l2,它們的斜率分別為k1、k2,l1與l2的交點P為“供給-需求”均衡點,在供求兩種力量的相互作用下,該商品的價格和產銷量,沿平行于坐標軸的“蛛網”路徑,箭頭所指方向發展變化,最終能否達于均衡點P,與直線l1、 l2的斜率滿足的條件有關,從下列三個圖中可知最終能達于均衡點P的條件為
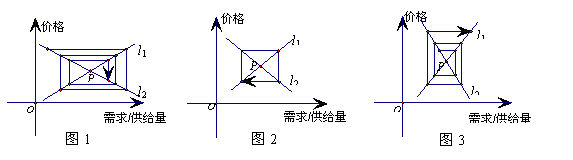
(A)k1+k2>0 (B)k1+k2=0 (C)k1+k2<0 (D)k1+k2可取任意實數
11.把函數f (x)=2sin( )cos(
)cos( )的圖象向左平移a(a>0)個單位,得到函數y=g (x)的圖象。若函數y= g (x)是奇函數,則a的最小值為
)的圖象向左平移a(a>0)個單位,得到函數y=g (x)的圖象。若函數y= g (x)是奇函數,則a的最小值為
(A) 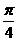 (B)
(B)  (C)
(C)  (D)
(D)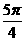
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com