
題目列表(包括答案和解析)
8、已知函數(shù)f(x) = 2x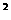 -x,則使得數(shù)列{
-x,則使得數(shù)列{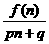 }(n∈N
}(n∈N )成等差數(shù)列的非零常數(shù)p與q所滿足的關系式為
.
)成等差數(shù)列的非零常數(shù)p與q所滿足的關系式為
.
7、已知函數(shù)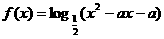 的值域為R,且f(x)在(
的值域為R,且f(x)在(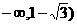 上是增函數(shù),則a的范圍是 .
上是增函數(shù),則a的范圍是 .
6、在一個棱長為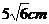 的正四面體內有一點P,它到三個面的距離分別是1cm,2cm,3cm,則它到第四個面的距離為_______________cm
.
的正四面體內有一點P,它到三個面的距離分別是1cm,2cm,3cm,則它到第四個面的距離為_______________cm
.
5、設等比數(shù)列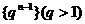 的前n項和為
的前n項和為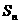 ,前n+1項的和為
,前n+1項的和為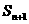 ,
,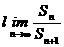 =______.
=______.
4、過雙曲線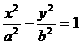 的右焦點F(c,0)的直線交雙曲線于M、N兩點,交y軸于P
的右焦點F(c,0)的直線交雙曲線于M、N兩點,交y軸于P
點,則有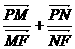 的定值為
的定值為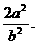 類比雙曲線這一結論,在橢圓
類比雙曲線這一結論,在橢圓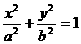 (a>b
(a>b
>0)中,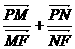 是定值
A.
是定值
A.
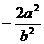 B.
B.
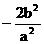 C.
C.
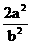 D.
D.
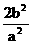
3、從-3,-2,-1,1,2,3中任取三個不同的數(shù)作為橢圓方程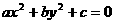 中的系
中的系
數(shù),則確定不同橢圓的個數(shù)為 A .17 B. 18 C. 19 D. 20
2、設奇函數(shù) 上是增函數(shù),且
上是增函數(shù),且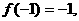 若函數(shù)
若函數(shù)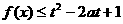 對所有
對所有
的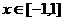 都成立,當
都成立,當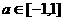 時,則t的取值范圍是
時,則t的取值范圍是
A.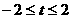 B.
B.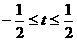
C.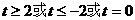 D.
D.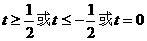
1、由方程 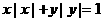 確定的函數(shù)y = f (x)在(-∞,+ ∞)上是
確定的函數(shù)y = f (x)在(-∞,+ ∞)上是
A.奇函數(shù) B.偶函數(shù) C.增函數(shù) D.減函數(shù)
14、(本題滿分12分)
(文)解:(1)直線l過點(3,-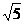 )且方向向量為
)且方向向量為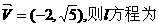
 ……………………………………(4分)
……………………………………(4分)
(2)設直線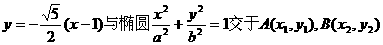 ,
,
由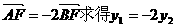 ……………………………………………………(7分)
……………………………………………………(7分)
將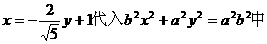 ,
,
整理得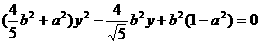
|
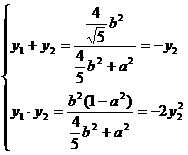 (9分)
(9分)
由①2/②知 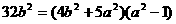 ……………………………………(12分)
……………………………………(12分)
又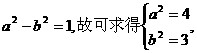 因此所求橢圓方程為:
因此所求橢圓方程為: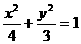 …(14分)
…(14分)
(理)解:(1)直線l過點(3,-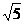 )且方向向量為
)且方向向量為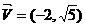

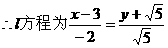
化簡為: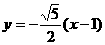 …………(4分)
…………(4分)
(2)設直線
交于兩點A(x1,y1),B(x2,y2),和x軸交于M(1,0)
由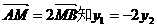 ………………………………………………(7分)
………………………………………………(7分)
將
…………………………………………①
|
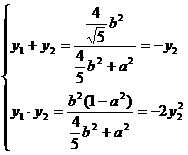
由②2/③ 知:32b2=(4b2+5a2)(a2-1)…………………………………………(10分)
化為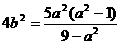 ………………………………………………④
………………………………………………④
對方程①求判別式,且由△>0
即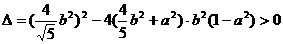
化簡為: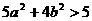 ………………………………………………⑤ 12分
………………………………………………⑤ 12分
由④式代入⑤可知: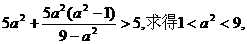 又橢圓的焦點在x軸上,
又橢圓的焦點在x軸上,
則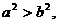 由④知:
由④知:
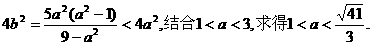
因此所求橢圓長軸長2a范圍為(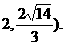 14分
14分
13、(本題滿分16分)
解:(Ⅰ)連結PB。∵線段BQ的垂直平分線與AQ交于點P,
∴|PB|=|PQ|,又|AQ|=6,
∴|PA|+|PB|=|PA|+|PQ|=|AQ|=6(常數(shù))。 …2分
又|PA|+|PB|>|AB|,從而P點的軌跡T是中心在原點,以A、B為兩個焦點,長軸在x軸上的橢圓,其中,2a=6,2c=4,
∴橢圓方程為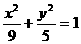 …6分
…6分
(Ⅱ)當直線l與x軸垂直時,MN的中點為R(2,0)
直線RS的縱截距t =0 …7分
當直線l與x軸不垂直時,設其斜率為k,
點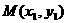 、
、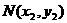 、
、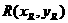 。
。
由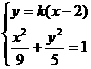 ,消去y整理得:
,消去y整理得:
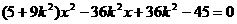 …9分
…9分
∴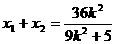 ,
,
則
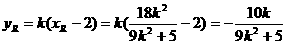
直線RS的方程為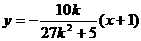 。
。
令x=0,可得直線RS的縱截距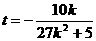 。
。
如果k=0,則t=0;
如果k≠0,則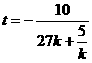 。
。
∵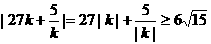
當且僅當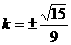 時,等號成立。
…14分
時,等號成立。
…14分
∴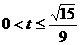 或
或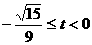
綜上可知,所求t的取值范圍是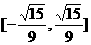 。
…16分
。
…16分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com