
題目列表(包括答案和解析)
有一項是符合題目要求的.)
1.設p、q是兩個命題,則“復合命題p或q為真,p且q為假”的充要條件是 ( )
A.p、q中至少有一個為真 B.p、q中至少有一個為假
C.p、q中有且只有一個為真 D.p為真,q為假
22.解(1)令m=-1,n=0則:f (–1)=f (–1)f (0),而f (–1)>1 ∴f(0)=1
令m=x>0,n= –x<0則f (x–x)=f (x)·f (–x)=1
∴f (x)=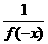
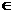 (0,1),即x>0時0<f (x)<1
(0,1),即x>0時0<f (x)<1
設x1<x2則x2–x1=0 ∴0<f (x2–x1)·f (x1)–f (x1)=f (x1)[f (x2–x1)–1]<0 ∴f(x)<f(x1)
即y = f (x)在R上單調遞減
(2)由f (an+1)=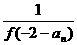 ,n
,n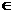 N* 得:f (an+1)·f (–2–an)
=1
N* 得:f (an+1)·f (–2–an)
=1
∴f (an+1–an–2) = f (0) 由(1)知:an+1–an–2=0
即an+1–an=2(n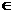 N*) ∴{an}是首項為a1=1,公差為2的等差數列
N*) ∴{an}是首項為a1=1,公差為2的等差數列
∴an=2n–1
(3)假設存在正數k,使(1+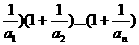
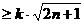 對n
對n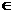 N*恒成立
N*恒成立
記F(n)=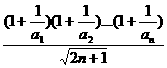
即 ∴F(n)是遞增數列,F(1)為最小值。
∴F(n)是遞增數列,F(1)為最小值。
由F(n) 恒成立知k
恒成立知k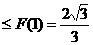 ∴kmax =
∴kmax = 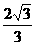 .
.
22.(本小題滿分14分)y = f
(x)的定義域為R,對任意實數m、n有f (m+n) =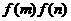 ,且當x<0時,
,且當x<0時,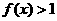 ,數列{an}滿足
,數列{an}滿足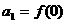 且
且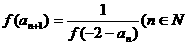 *)。
(1)求證:y = f
(x)在R上單調遞減;
(2)求數列{an}的通項公式;
(3)是否存在正數k,使
*)。
(1)求證:y = f
(x)在R上單調遞減;
(2)求數列{an}的通項公式;
(3)是否存在正數k,使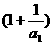 ·
·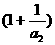 …
…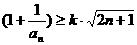 ,對一切n∈N*均成立,若存在,試求出k的最大值并證明,若不存在,說明理由。
,對一切n∈N*均成立,若存在,試求出k的最大值并證明,若不存在,說明理由。
21. 解:(I)由已知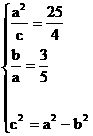 ,解之得:
,解之得: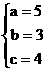 …………(3分)
…………(3分)
∴橢圓的方程為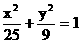 ,雙曲線的方程
,雙曲線的方程
又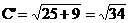
∴雙曲線的離心率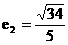 ………………(7分)
………………(7分)
(II)由(I)
設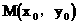 則由
則由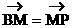 得M為BP的中點
得M為BP的中點
∴P點坐標為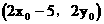
將M、P坐標代入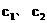 方程得:
方程得:
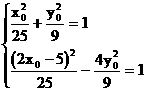
消去 得:
得: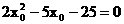
解之得: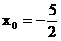 或
或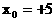 (舍)
(舍)
由此可得: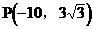 ………………(9分)
………………(9分)
當P為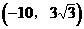 時,
時,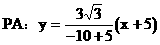
即: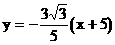
代入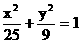 ,得:
,得: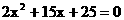
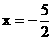 或
或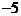 (舍)
(舍)
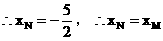
MN⊥x軸,即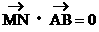 ………………(14分)
………………(14分)
21.(本小題滿分12分)已知橢圓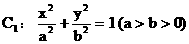 的一條準線方程是
的一條準線方程是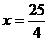 ,其左、右頂點分別是A、B;雙曲線
,其左、右頂點分別是A、B;雙曲線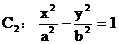 的一條漸近線方程為
的一條漸近線方程為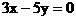 。
。
(I)求橢圓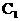 的方程及雙曲線
的方程及雙曲線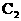 的離心率;
的離心率;
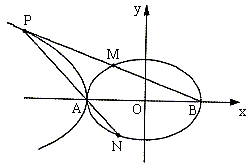
(II)在第二象限內取雙曲線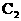 上一點P,連結BP交橢圓
上一點P,連結BP交橢圓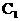 于點M,連結PA并延長交橢圓
于點M,連結PA并延長交橢圓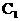 于點N,若
于點N,若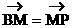 。求證:
。求證: 。
。
20. (本小題滿分12分)某廠家擬在2005年國慶節期間舉行促銷活動,經調查測算,該產品的年銷量(即該廠的年產量)x萬件與年促銷費用m萬元(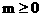 )滿足
)滿足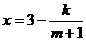 (k為常數),如果不搞促銷活動,該產品的年銷售量只能是1萬件,已知2005年生產該產品的固定投入為8
(k為常數),如果不搞促銷活動,該產品的年銷售量只能是1萬件,已知2005年生產該產品的固定投入為8
萬元,每生產1萬件產品需要投入16萬元,廠家將每件產品的銷售價格定
為年平均每件產品成本的1.5倍(產品成本包括固定投入和再投入兩部分
資金)
(1)將2005年該產品的利潤y萬元表示為年促銷費用m萬元的函數;
(2)該廠家2005年的促銷費用投入多少萬元時,廠家的年利潤最大?
解:(1)設2005年生產產品x萬件
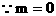 時,
時,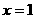 代入
代入
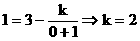 ………………(2分)
………………(2分)
則年成本: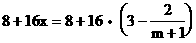 ………………(4分)
………………(4分)
年利潤: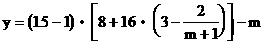 …………(6分)
…………(6分)
 ……………………(7分)
……………………(7分)
(2)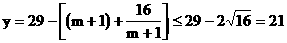 ………………(10分)
………………(10分)
當且僅當 ,即
,即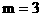 時取等號………………(11分)
時取等號………………(11分)
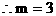 時,
時,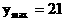 萬元……………………(12分)
萬元……………………(12分)
19.(本小題滿分12分)已知函數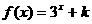 (k為常數),A(-2k, 2)是函數
(k為常數),A(-2k, 2)是函數 圖象上的點。
圖象上的點。
(I)求實數k的值及函數 的解析式;
的解析式;
(II)將 的圖象按向量
的圖象按向量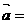 (3,0)平移,得到函數y=g(x)的圖象。若
(3,0)平移,得到函數y=g(x)的圖象。若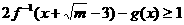 恒成立,試求實數m的取值范圍。
恒成立,試求實數m的取值范圍。
解:(I)∵A(-2k, 2)是函數y=f-1(x)圖象上的點。
∴B(2,-2K)是函數y=f(x)上的點。 ∴2k=32+k
∴k=-3, ∴y=f(x)=3x-3 ∴y=f-1(x)=log3(x+3),(x>-3)
(II)將y=f-1(x)的圖象按向量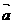 =(3,0)平移,得函數y=g(x)=log3x(x>0)
=(3,0)平移,得函數y=g(x)=log3x(x>0)
要使2f-1(x+ )-g(x)≥1 恒成立, 即使2log3(x+
)-g(x)≥1 恒成立, 即使2log3(x+ )-log3x≥1恒成立。
)-log3x≥1恒成立。
所以有x+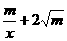 ≥3在x>0時恒成立,只須(x+
≥3在x>0時恒成立,只須(x+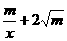 )min≥3。
)min≥3。
又x+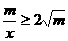 (當且僅當x=
(當且僅當x=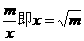 時取等號)
時取等號)
∴(x+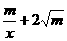 )min=4
)min=4 只須4
只須4 ≥3,即m≥
≥3,即m≥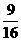 。
。
∴實數m的取值范圍為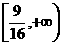
18.(本小題滿分12分)已知函數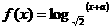 的圖象經過原點。
的圖象經過原點。
(1)若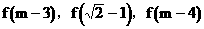 成等差數列,求m的值;
成等差數列,求m的值;
(2)若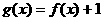 ,正數a、b、c成等比數列,求證:
,正數a、b、c成等比數列,求證:
解:(1)將(0,0)代入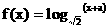 ,得:
,得: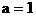
 ………………(2分)
………………(2分)
由已知可得: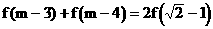 ………………(3分)
………………(3分)
即: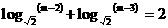
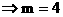 (
(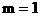 舍)……………………(6分)
舍)……………………(6分)
(2)由已知可得: 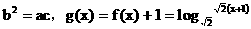
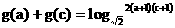
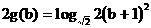 …(8分)
…(8分)
而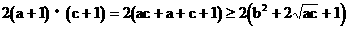
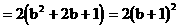
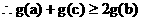 …(12分)
…(12分)
另解: ………(8分)
………(8分)
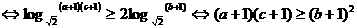
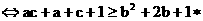 ………………(10分)
………………(10分)
∵a,b,c成等比數列 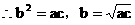
 得證(12分)
得證(12分)
17.(本小題滿分12分)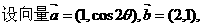
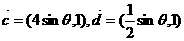 ,其中
,其中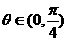 。
。
(I)求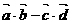 的取值范圍;
的取值范圍;
(II)若函數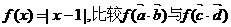 的大小。
的大小。
解:
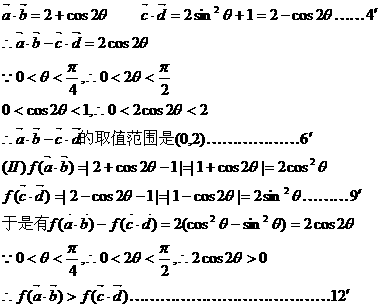
16.給出以下結論:
①通項公式為an=a1(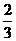 )n-1的數列一定是以a1為首項,
)n-1的數列一定是以a1為首項,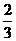 為公比的等比數列;
為公比的等比數列;
②存在角α使得tanα+cotα=-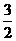 成立;
成立;
③函數y=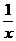 在定義域上是單調遞減的;
在定義域上是單調遞減的;
④若α,β∈(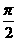 ,π),且tanα<cotβ,則α+β<
,π),且tanα<cotβ,則α+β<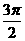 ;
;
⑤函數y=log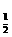 (4-x2)的值域是
(4-x2)的值域是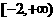 .
.
其中可能成立的結論的序號是__4.5________.(注:把你認為正確的命題的序號都填上)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com