
題目列表(包括答案和解析)
2、方程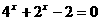 的解是__________.
的解是__________.
見理2
1、函數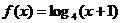 的反函數
的反函數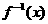 =__________.
=__________.
見理1
(17)(本小題滿分12分)
已知向量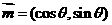 和
和 ,且
,且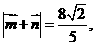 求
求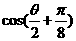 的值.
的值.
(18)(本小題滿分12分)
袋中裝有黑球和白球共7個,從中任取2個球都是白球的概率為 現有甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到兩人中有一人取到白球時既終止,每個球在每一次被取出的機會是等可能的,用
現有甲、乙兩人從袋中輪流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到兩人中有一人取到白球時既終止,每個球在每一次被取出的機會是等可能的,用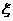 表示取球終止所需要的取球次數.
表示取球終止所需要的取球次數.
(I)求袋中原有白球的個數;
(II)求隨機變量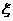 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
(19)(本小題滿分12分)
已知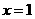 是函數
是函數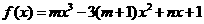 的一個極值點,其中
的一個極值點,其中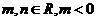 ,
,
(I)求 與
與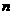 的關系式;
的關系式;
(II)求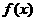 的單調區間;
的單調區間;
(III)當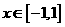 時,函數
時,函數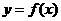 的圖象上任意一點的切線斜率恒大于3
的圖象上任意一點的切線斜率恒大于3 ,求
,求 的取值范圍.
的取值范圍.
(20)(本小題滿分12分)
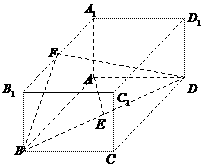 如圖,已知長方體
如圖,已知長方體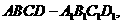
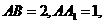 直線
直線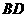 與平面
與平面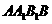 所成的角為
所成的角為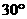 ,
,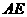 垂直
垂直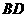 于
于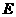 ,
,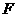 為
為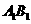 的中點.
的中點.
(I)求異面直線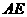 與
與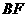 所成的角;
所成的角;
(II)求平面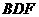 與平面
與平面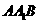 所成的二面角;
所成的二面角;
(III)求點 到平面
到平面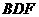 的距離.
的距離.
(21)(本小題滿分12分)
已知數列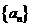 的首項
的首項 前
前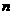 項和為
項和為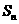 ,且
,且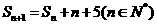
(I)證明數列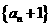 是等比數列;
是等比數列;
(II)令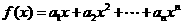 ,求函數
,求函數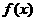 在點
在點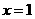 處的導數
處的導數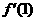 并比較
并比較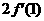 與
與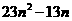 的大小.
的大小.
(22)(本小題滿分14分)
已知動圓過定點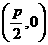 ,且與直線
,且與直線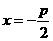 相切,其中
相切,其中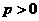 .
.
(I)求動圓圓心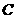 的軌跡的方程;
的軌跡的方程;
(II)設A、B是軌跡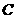 上異于原點
上異于原點 的兩個不同點,直線
的兩個不同點,直線 和
和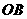 的傾斜角分別為
的傾斜角分別為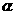 和
和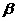 ,當
,當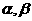 變化且
變化且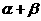 為定值
為定值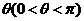 時,證明直線
時,證明直線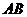 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
(13)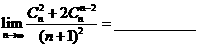 .
.
(14)設雙曲線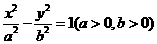 的右焦點為
的右焦點為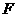 ,右準線
,右準線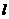 與兩條漸近線交于P、
與兩條漸近線交于P、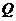 兩點,如果
兩點,如果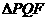 是直角三角形,則雙曲線的離心率
是直角三角形,則雙曲線的離心率 .
.
(15)設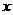 、
、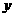 滿足約束條件
滿足約束條件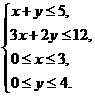 則使得目標函數
則使得目標函數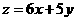 的最大的點
的最大的點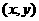 是____________
是____________
(16)已知 是不同的直線,
是不同的直線,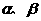 是不重合的平面,給出下列命題:①若
是不重合的平面,給出下列命題:①若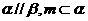 ,
,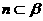 則
則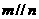 ;②若
;②若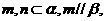 則
則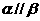 ③若
③若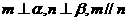 ,則
,則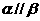 ④
④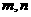 是兩條異面直線,若
是兩條異面直線,若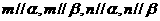 ,則
,則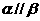
上面的命題中,真命題的序號是 (寫出所有真命題的序號)
(寫出所有真命題的序號)
(1)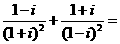
(A) (B)
(B)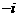 (C)1 (D)
(C)1 (D)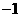
(2)函數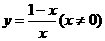 的反函數圖像大致是
的反函數圖像大致是
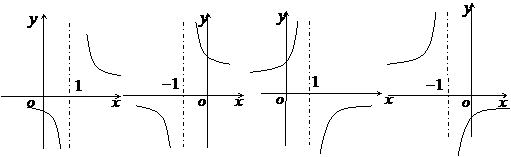
(A) (B) (C) (D)
(3)已知函數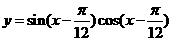 ,則下列判斷正確的是
,則下列判斷正確的是
(A)此函數的最小周期為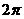 ,其圖像的一個對稱中心是
,其圖像的一個對稱中心是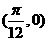
(B)此函數的最小周期為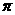 ,其圖像的一個對稱中心是
,其圖像的一個對稱中心是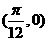
(C)此函數的最小周期為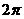 ,其圖像的一個對稱中心是
,其圖像的一個對稱中心是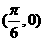
(D)此函數的最小周期為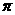 ,其圖像的一個對稱中心是
,其圖像的一個對稱中心是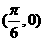
(4)下列函數既是奇函數,又在區間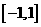 上單調遞減的是
上單調遞減的是
(A)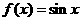 (B)
(B)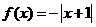 (C)
(C)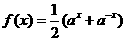 (D)
(D)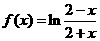
(5)如果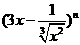 的展開式中各項系數之和為128,則展開式中
的展開式中各項系數之和為128,則展開式中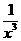 的系數是
的系數是
(A)7
(B)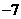 (C)21
(D)
(C)21
(D)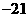
(6)函數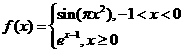 ,若
,若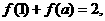 則
則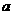 的所有可能值為
的所有可能值為
(A)1
(B)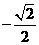 (C)
(C)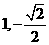 (D)
(D)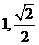
(7)已知向量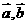 ,且
,且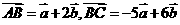 ,
,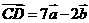 ,則一定共線的三點是
,則一定共線的三點是
(A)A、B、D (B)A、B、C (C)B、C、D (D)A、C、D
(8)設地球的半徑為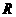 ,若甲地位于北緯
,若甲地位于北緯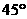 東經
東經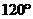 ,乙地位于南緯
,乙地位于南緯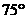 東經
東經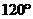 ,則甲、乙兩地的球面距離為
,則甲、乙兩地的球面距離為
(A)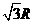 (B)
(B)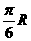 (C)
(C)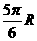 (D)
(D)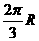
(9)10張獎券中只有3張有獎,5個人購買,至少有1人中獎的概率是
(A)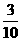 (B)
(B)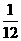 (C)
(C)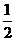 (D)
(D)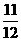
(10)設集合A、B是全集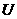 的兩個子集,則
的兩個子集,則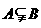 是
是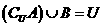 的
的
(A)充分不必要條件(B)必要不充分條件(C)沖要條件(D)既不充分也不必要條件
(11)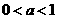 ,下列不等式一定成立的是
,下列不等式一定成立的是
(A)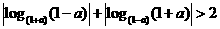
(B)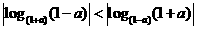
(C)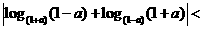
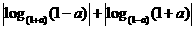
(D)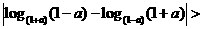
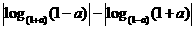
(12)設直線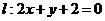 關于原點對稱的直線為
關于原點對稱的直線為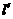 ,若
,若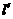 與橢圓
與橢圓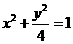 的交點為A、B、,點
的交點為A、B、,點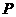 為橢圓上的動點,則使
為橢圓上的動點,則使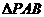 的面積為
的面積為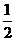 的點
的點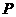 的個數為
的個數為
(A)1 (B)2 (C)3 (D)4
第II卷(共90分)
22. (本小題滿分14分)
設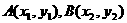 兩點在拋物線
兩點在拋物線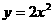 上,
上,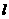 是AB的垂直平分線,
是AB的垂直平分線,
(Ⅰ)當且僅當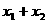 取何值時,直線
取何值時,直線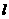 經過拋物線的焦點F?證明你的結論;
經過拋物線的焦點F?證明你的結論;
(Ⅱ)當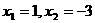 時,求直線
時,求直線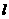 的方程.
的方程.
21. (本小題滿分12分)
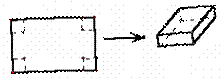
用長為90cm,寬為48cm的長方形鐵皮做一個無蓋的容器,先在四角分別截去一個小
正方形,然后把四邊翻轉90°角,再焊接而成(如圖),問該容器的高為多少時,容器的容積最
大?最大容積是多少?
……
20.(本小題滿分12分)
在等差數列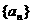 中,公差
中,公差 的等差中項.
的等差中項.
已知數列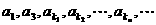 成等比數列,求數列
成等比數列,求數列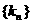 的通項
的通項
19.(本小題滿分12分)
在四棱錐V-ABCD中,底面ABCD是正方形,側面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)證明AB⊥平面VAD;
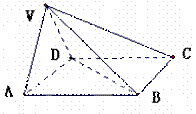 (Ⅱ)求面VAD與面VDB所成的二面角的大小.
(Ⅱ)求面VAD與面VDB所成的二面角的大小.
18.(本小題滿分12分)
設甲、乙、丙三臺機器是否需要照顧相互之間沒有影響。已知在某一小時內,甲、
乙都需要照顧的概率為0.05,甲、丙都需要照顧的概率為0.1,乙、丙都需要照顧的概
率為0.125,
(Ⅰ)求甲、乙、丙每臺機器在這個小時內需要照顧的概率分別是多少;
(Ⅱ)計算這個小時內至少有一臺需要照顧的概率.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com